Coders Strikes Back

1 Introduction

Ce document est la pour expliquer comment créer une "bonne" intelligence articielle pour le jeu "Coders strike back" de CodinGame. Je vais essayer de garder ce document agnostique par rapport au langage de programmation que vous voulez utiliser. Il n'y aura donc que du "pseudo code" et pas de vrais morceaux de codes. Ce pseudo code ressemblera à 95% à du C++ car c'est le langage que j'ai utilisé. Ne vous attendez pas à trouver des classes entières que vous pourrez copier/coller, si vous voulez mettre en application ce que vous trouverez ici, il va falloir coder.

2 Pré requis

Voici les quelques notions que vous devez connaître pour ne pas complètement être perdu en lisant ce document :

3 Conception

Avant d'aller plus loin, le plus simple est de faire un diagramme de classes UML pour présenter les classes que j'utilises.

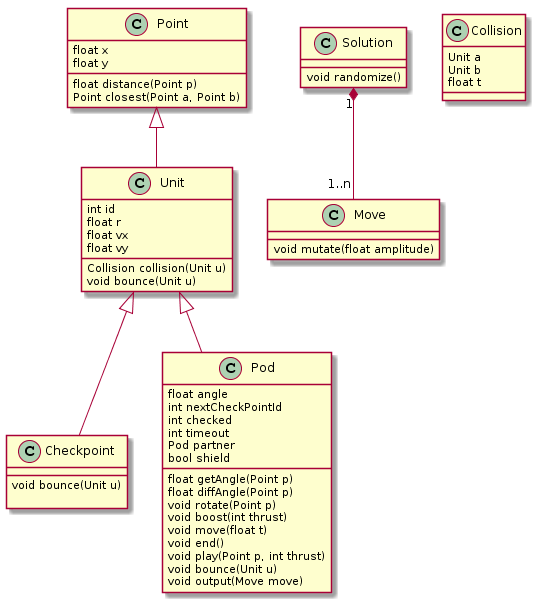
Avec quelques explications en détails :

Quelques précisions :

4 Simulation

Pour faire une intelligence artifielle efficace, on est obligé de savoir simuler les prochains tours pour prédire ce qu'il va arriver. Au minimum il faut savoir prédire les mouvements. Savoir prédire les collisions est encore mieux bien sur, mais c'est plus compliqué.

Nous allons commencer par les mouvements qui sont plus simples. Dans un tour, chaque pod va effectuer les actions suivantes et dans cet ordre :

Afin de faire des simulations facilement, je vous conseil de cloner tous les pods que vous avez au début d'un tour. Cela vous permettra de revenir très vite à l'état initial après avoir fait une simulation de plusieurs tours. Certains langages ont des méthodes clone de base, sinon il faudra la coder vous-même.

4.1 Quelques rappels

Avant de rentrer dans le vif du sujet. Voici le pseudo code de quelques méthodes utilitaires simples de mes classes :

4.1.1 Méthodes distance et distance2 de Point

float distance2(Point p) {
    return (this.x - p.x)*(this.x - p.x) + (this.y - p.y)*(this.y - p.y);
}

float distance(Point p) {
    return sqrt(this.distance2(p));
}

Pourquoi 2 fonctions de distance ? Tout simplement parce sqrt est lent, quelque soit le langage. Il vaut mieux l'éviter si on en a pas vraiment besoin. Et parfois on a besoin de la distance au carré dans certains calculs, donc on appellera distance2 directement.

4.2 Rotation

Pour savoir comment un pod va tourner, il faut déjà savoir la différence d'angle entre l'angle actuel du pod et le point visé. L'angle actuel du pod est donné dans les inputs du programme entre 0 et 359. 0 veut dire que le pod regarde plein est. 90 c'est plein sud. 180 plein ouest. Et enfin 270 plein nord. Voici le pseudo code de la méthode getAngle(Point p) de la classe Pod :

float getAngle(Point p) {
    float d = this.distance(p);
    float dx = (p.x - this.x) / d;
    float dy = (p.y - this.y) / d;

    // Trigonométrie simple. On multiplie par 180.0 / PI pour convertir en degré.
    float a = acos(dx) * 180.0 / PI;

    // Si le point qu'on veut est en dessus de nous, il faut décaler l'angle pour qu'il soit correct.
    if (dy < 0) {
        a = 360.0 - a;
    }

    return a;
}

Cette fonction renvoie l'angle que devrait avoir le pod pour faire face au point donné. Donc si le point se trouve par exemple exactement en haut à droite du pod, cette fonction donnera 315. Il faut ensuite savoir de combien (et dans quel sens) le pod doit tourner pour viser ce point. C'est le but de la méthode diffAngle :

float diffAngle(Point p) {
    float a = this.getAngle(p);

    // Pour connaitre le sens le plus proche, il suffit de regarder dans les 2 sens et on garde le plus petit
    // Les opérateurs ternaires sont la uniquement pour éviter l'utilisation d'un operateur % qui serait plus lent
    float right = this.angle <= a ? a - this.angle : 360.0 - this.angle + a;
    float left = this.angle >= a ? this.angle - a : this.angle + 360.0 - a;

    if (right < left) {
        return right;
    } else {
        // On donne un angle négatif s'il faut tourner à gauche
        return -left;
    }
}

Nous avons donc un angle et un sens pour tourner vers un point. Le sens est donné par le signe du résultat. S'il est négatif, alors on doit tourner vers la gauche, sinon c'est vers la droite. Il ne reste plus qu'à vraiment tourner et c'est la méthode rotate qui le fait :

void rotate(Point p) {
    float a = this.diffAngle(p);

    // On ne peut pas tourner de plus de 18° en un seul tour
    if (a > 18.0) {
        a = 18.0;
    } else if (a < -18.0) {
        a = -18.0;
    }

    this.angle += a;

    // L'opérateur % est lent. Si on peut l'éviter, c'est mieux.
    if (this.angle >= 360.0) {
        this.angle = this.angle - 360.0;
    } else if (this.angle < 0.0) {
        this.angle += 360.0;
    }
}

4.3 Appliquer le thrust

Une fois que le pod a tourné, il faut maintenant appliquer le thrust. C'est le rôle de la méthode boost :

void boost(int thrust) {
    // N'oubliez pas qu'un pod qui a activé un shield ne peut pas accélérer pendant 3 tours
    if (this.shield) {
        return;
    }

    // Conversion de l'angle en radian
    float ra = this.angle * PI / 180.0;

    // Trigonométrie
    this.vx += cos(ra) * thrust;
    this.vy += sin(ra) * thrust;
}

4.4 Se déplacer

Il ne reste plus qu'à déplacer le pod avec la méthode move :

void move(float t) {
    this.x += this.vx * t;
    this.y += this.vy * t;
}

A quoi sert le paramètre t ? Il servira plus tard quand on voudra simuler un tour entier en prenant en compte les collisions. Il sert à indiquer de combien le pod doit avancer. Si t vaut 1.0, alors le pod va avancer d'un tour entier. S'il vaut 0.5, alors il n'avancera que de la moitié d'un tour. Si vous ne simulez pas les collisions, alors vous pouvez toujours mettre 1.0 à la place de t.

4.5 Après le déplacement

Une fois que le pod s'est déplacé, il faut appliquer la friction et arrondir (ou tronquer) des valeurs. C'est que fait ma méthode end :

void end() {
    this.x = round(this.x);
    this.y = round(this.y);
    this.vx = truncate(this.vx * 0.85);
    this.vy = truncate(this.vy * 0.85);

    // N'oubliez pas que le timeout descend de 1 chaque tour. Il revient à 100 quand on passe par un checkpoint
    this.timeout -= 1;
}

Attention : Ici c'est du pseudo code, truncate n'existe pas. Mais si vous ne voulez pas avoir de problème d'arrondis, je vous conseil de ne pas utiliser floor. Pourquoi ? C'est très simple, exécuter ce code dans le langage de votre choix :

print(floor(1.5));
print(floor(-1.5));

La sortie devrait ressembler à quelque chose comme 1.0 -2.0. Et oui, floor ne marche pas comme on le voudrait sur les nombres négatifs. Si votre langage le permet, il est mieux de simplement caster this.vx et this.vy en entier, cela tronquera purement et simplement la partie après la virgule. Si vous ne pouvez pas, il faut faire un if pour utiliser floor ou ceil suivant le cas.

4.6 Jouer un déplacement en entier

Vous êtes maintenant capable de faire jouer le déplacement complet d'un pod et donc prédire à quelle position un pod sera au prochain tour s'il vise un point spécifique. C'est la méthode play :

void play(Point p, int thrust) {
    this.rotate(p);
    this.boost(thrust);
    this.move(1.0);
    this.end();
}

Vous n'êtes pas encore capable de prédire les collisions et leurs effets, mais juste avec ça, vous pouvez tester plusieurs angles et vitesses et choisir la meilleure. Si vous faites des prédictions sur plusieurs tours pour choisir le meilleur chemin pour vos pods, vous devriez atteindre le top 50 sans problème.

4.7 Prédire une collision

Nous rentrons maintenant dans la partie la plus compliqué pour simuler un tour complètement : les collisions. Nous avons 2 objets de classe Unit et nous voulons savoir si et quand ces 2 objets vont entrer en collision dans le tour. C'est ce que fait la méthode collision de Unit. Mais avant d'entrer dans le code en détail, un peu de théorie.

Déjà il y a des collisions qu'on peut détecter immédiatement car les 2 objets sont déjà assez proches l'un de l'autre. Si la distance entre les 2 objets est inférieure à la somme des rayons, alors on a une collision immédiatement.

Ensuite, comment détecter que 2 objets en mouvement vont entrer en collision ? Déjà on peut simplifier le problème. Il faut changer de référentiel et se placer dans le référentiel de l'une des 2 unités. De cette façon le problème est plus simple : comment détecter qu'un objet en mouvement va entrer en collision avec un objet immobile ? C'est la qu'entre en jeu la géométrie.

L'objet qui se déplace le fait forcément sur une droite. Pour savoir si les objets vont entrer en collision, il faut regarder la distance entre notre objet immobile et son point le plus proche sur cette droite. Si cette distance est inférieur à la somme des rayons des 2 objets, alors nous avons une chance de collision. Pour confirmer cette chance de collision, il faut ensuite regarder la vitesse de l'objet qui se déplace (pour vérifier s'il s'éloigne ou s'il se rapproche de l'objet immobile). Et s'il se rapproche il faut regarder dans combien de temps il va atteindre l'objet immobile. Si une collision se passe à un temps t supérieur à 1.0, cela veut dire qu'elle se passera dans plus d'un tour et on peut donc l'ignorer.

Pour commencer, voici le code de la méthode closest de Point. Elle permet de trouver le point le plus proche sur une droite (décrite ici par 2 points) depuis un point.

Point closest(Point a, Point b) {
    float da = b.y - a.y;
    float db = a.x - b.x;
    float c1 = da*a.x + db*a.y;
    float c2 = -db*this.x + da*this.y;
    float det = da*da + db*db;
    float cx = 0;
    float cy = 0;

    if (det != 0) {
        cx = (da*c1 - db*c2) / det;
        cy = (da*c2 + db*c1) / det;
    } else {
        // Le point est déjà sur la droite
        cx = this.x;
        cy = this.y;
    }

    return new Point(cx, cy);
}

Maintenant nous pouvons passer au code de la méthode collision de Unit : 

Collision collision(Unit u) {
    // Distance carré
    float dist = this.distance2(u);

    // Somme des rayons au carré
    float sr = (this.r + u.r)*(this.r + u.r);

    // On prend tout au carré pour éviter d'avoir à appeler un sqrt inutilement. C'est mieux pour les performances

    if (dist < sr) {
        // Les objets sont déjà l'un sur l'autre. On a donc une collision immédiate
        return new Collision(this, u, 0.0);
    }

    // Optimisation. Les objets ont la même vitesse ils ne pourront jamais se rentrer dedans
    if (this.vx == u.vx && this.vy == u.vy) {
        return null;
    }

    // On se met dans le référentiel de u. u est donc immobile et se trouve sur le point (0,0) après ça
    float x = this.x - u.x;
    float y = this.y - u.y;
    Point myp = new Point(x, y);
    float vx = this.vx - u.vx;
    float vy = this.vy - u.vy;
    Point up = new Point(0, 0)

    // On cherche le point le plus proche de u (qui est donc en (0,0)) sur la droite décrite par notre vecteur de vitesse
    Point p = up.closest(myp, new Point(x + vx, y + vy));

    // Distance au carré entre u et le point le plus proche sur la droite décrite par notre vecteur de vitesse
    float pdist = up.distance2(p);

    // Distance au carré entre nous et ce point
    float mypdist = myp.distance2(p);

    // Si la distance entre u et cette droite est inférieur à la somme des rayons, alors il y a possibilité de collision
    if (pdist < sr) {
        // Notre vitesse sur la droite
        float length = sqrt(vx*vx + vy*vy);

        // On déplace le point sur la droite pour trouver le point d'impact
        float backdist = sqrt(sr - pdist);
        p.x = p.x - backdist * (vx / length);
        p.y = p.y - backdist * (vy / length);

        // Si le point s'est éloigné de nous par rapport à avant, c'est que notre vitesse ne va pas dans le bon sens
        if (myp.distance2(p) > mypdist) {
            return null;
        }

        pdist = p.distance(myp);

        // Le point d'impact est plus loin que ce qu'on peut parcourir en un seul tour
        if (pdist > length) {
            return null;
        }

        // Temps nécessaire pour atteindre le point d'impact
        float t = pdist / length;

        return new Collision(this, u, t);
    }

    return null;
}

Avec cette méthode, on peut donc savoir si 2 objets de type Unit vont avoir une collision pendant le tour et surtout quand.

4.8 Les effets d'une collision

Ici il faut séparer plusieurs types de collision. Il y a d'abord une collision très simple à gérer, c'est celle d'un Pod avec un Checkpoint. Il n'y a pas de rebond, on doit juste s'assurer d'incrémenter le compteur des checkpoints passés pour le pod et de remettre le timeout du pod à 100.

Maintenant le cas complexe : 2 pods se rentrent dedans. Les collisions dans ce contest sont des collisions élastiques parfaites avec une demi impulsion de 120 minimum. Vous n'avez rien compris ? Moi non plus. Pour être franc, je n'aurais jamais trouvé ce code sans l'aide de Neumann et de pb4608. Mais je vous donne quand même le code de ma fonction bounce de Pod

void bounce(Unit u) {
    if (u instanceof Checkpoint) {
        // On entre en collision avec un checkpoint
        this.bounceWithCheckpoint((Checkpoint) u);
    } else {
        // Si un pod a son bouclier d'activé, sa masse est de 10, sinon elle est de 1
        float m1 = this.shield ? 10 : 1;
        float m2 = u.shield ? 10 : 1;

        // Si les masses sont égales, le coefficient sera de 2. Sinon il sera de 11/10
        float mcoeff = (m1 + m2) / (m1 * m2);

        float nx = this.x - u.x;
        float ny = this.y - u.y;

        // Distance au carré entre les 2 pods. Cette valeur pourrait être écrite en dure car ce sera toujours 800²
        float nxnysquare = nx*nx + ny*ny;

        float dvx = this.vx - u.vx;
        float dvy = this.vy - u.vy;

        // fx et fy sont les composantes du vecteur d'impact. product est juste la pour optimiser
        float product = nx*dvx + ny*dvy;
        float fx = (nx * product) / (nxnysquare * mcoeff);
        float fy = (ny * product) / (nxnysquare * mcoeff);

        // On applique une fois le vecteur d'impact à chaque pod proportionnellement à sa masse
        this.vx -= fx / m1;
        this.vy -= fy / m1;
        u.vx += fx / m2;
        u.vy += fy / m2;

        // Si la norme du vecteur d'impact est inférieur à 120, on change sa norme pour le mettre à 120
        float impulse = sqrt(fx*fx + fy*fy);
        if (impulse < 120.0) {
            fx = fx * 120.0 / impulse;
            fy = fy * 120.0 / impulse;
        }

        // On applique une deuxième fois le vecteur d'impact à chaque pod proportionnellement à sa masse
        this.vx -= fx / m1;
        this.vy -= fy / m1;
        u.vx += fx / m2;
        u.vy += fy / m2;

        // C'est l'un des rares endroits où avoir une classe Vector aurait rendu le code beaucoup plus lisible.
        // Mais cet endroit est appellé beaucoup trop souvent dans mon code pour que je me permette de le rendre plus lisible au prix de la performance
    }
}

Attention : Cette méthode repose sur l'hypothèse que les 2 pods se sont déplacés jusqu'à leur point d'impact respectifs. L'explication sur comment faire avancer les pods et jouer les collisions dans le but de simuler un tour complet se trouve dans le chapitre "Simuler un tour complet"

4.9 Les effets du bouclier

Comme indiqué en commentaire dans la fonction bounce du chapitre précédent, le seul effet du bouclier est de multiplier la masse d'un pod par 10. Ce qui fait que quand un pod avec bouclier cogne sur un pod sans bouclier, le vecteur d'impact s'appliquera 10 fois moins sur lui. N'oubliez pas que le bouclier empêche le pod d'accélérer pendant 3 tours après le bouclier. Il peut donner le thrust qu'il veut, il n'est pas pris en compte. Vous pouvez faire un autre bouclier pendant ces 3 tours, mais évidemment le compteur des 3 tours est relancé. Le bouclier n'a absolument aucune influence sur la vitesse d'un pod.

4.10 Prédire qu'un pod va passer par un checkpoint

C'est la raison pour laquelle ma classe Checkpoint hérite de Unit. Passer par un checkpoint n'est pas plus compliqué que d'entrer en collision avec lui. A la différence qu'il n'y a pas de rebond à gérer. Il suffit d'augmenter le nombre de checkpoints passés et de remettre le timeout à 100.

4.11 Simuler un tour complet

Avec toutes les méthodes décrites précédemment, on peut simuler un tour complet de jeu. Comment procéder ? Il faut d'abord regarder toutes les collisions qui vont avoir lieu pendant le tour et garder celle qui va arriver le plus tôt. On déplace ensuite les pods jusqu'à l'instant t de cette collision. On joue ensuite la collision. Et on recommence jusqu'à ce qu'on ait plus de collision à jouer (et on peut donc déplacer les pods jusqu'à la fin du tour). Mais attention, quand on joue une collision, il faut recalculer les collisions possibles. Parce qu'une collision entre 2 Unit peut empêcher d'autres collisions mais aussi en créer de nouvelles.

Pour recalculer les nouvelles collisions il y a 2 méthodes :

Sur le papier, la 2ème solution parait la plus performante. Mais dans les faits, j'ai eu de meilleurs résultats en utilisant la première. La raison est que dans ce contest, il n'y a pas assez de collisions en un seul tour pour que ce soit plus rapide avec la 2ème solution. Par contre si vous voulez appliquer ce principe à un jeu comme Poker Chip Race, je vous conseil grandement d'utiliser la 2ème solution.

Avec ces principes en tête, on peut écrire le code de la fonction play qui va simuler un tour complet.

void play(Pod[] pods, Checkpoint[] checkpoints) {
    // Il faut conserver le temps où on en est dans le tour. Le but est d'arriver à 1.0
    float t = 0.0;

    while (t < 1.0) {
        Collision firstCollision = null;

        // On cherche toutes les collisions qui vont arriver pendant ce tour
        for (int i = 0; i < pods.length; ++i) {
            // Collision avec un autre pod ?
            for (int j = i + 1; j < pods.length; ++j) {
                Collision col = pods[i].collision(pods[j]);

                // Si la collision arrive plus tôt que celle qu'on, alors on la garde
                if (col != null && col.t + t < 1.0 && (firstCollision == null || col.t < firstCollision.t)) {
                    firstCollision = col;
                }
            }

            // Collision avec un checkpoint ?
            // Inutile de tester toutes les checkpoints ici. On test juste le prochain checkpoint du pod.
            // On pourrait chercher les collisions du pod avec tous les checkpoints, mais si une telle collision arrive elle n'aura aucun impact sur le jeu de toutes façons
            Collision col = pods[i].collision(checkpoints[pods[i].nextCheckpointId]);

            // Si la collision arrive plus tôt que celle qu'on, alors on la garde
            if (col != null && col.t + t < 1.0 && (firstCollision == null || col.t < firstCollision.t)) {
                firstCollision = col;
            }
        }

        if (firstCollision == null) {
            // Aucune collision, on peut juste déplacer les pods jusqu'à la fin du tour
            for (int i = 0; i < pods.length; ++i) {
                pods[i].move(1.0 - t);
            }

            // Fin du tour
            t = 1.0;
        } else {
            // On bouge les pods du temps qu'il faut pour arriver sur l'instant `t` de la collision
            for (int i = 0; i < pods.length; ++i) {
                pods[i].move(firstCollision.t);
            }

            // On joue la collision
            firstCollision.a.bounce(firstCollision.b);

            t += firstCollision.t;
        }
    }

    // On arrondi les positions et on tronque les vitesses pour tout le monde
    for (int i = 0; i < pods.length; ++i) {
        pods[i].end();
    }
}

Optimisations possibles :

Bugs possibles :

4.12 Simuler ce qui arrivera

Avec la fonction du chapitre précédent, vous pouvez simuler un tour complet. Mais si vous avez été attentif, vous avez remarqué que vous simulez un tour avec des pods qui ne font rien du tout (ils gardent le même angle et n'accélèrent pas). C'est utile mais pas très intéressant. Nous ce qu'on veut c'est tester ce qui arrivera si on fait tel ou tel mouvement. Voici un code simple que vous pouvez adapter qui va simuler le tour complet en partant du principe que les pods vont tous viser le point en (8000, 4500) avec une vitesse de 200 :

void test(Pod[] pods, Checkpoint[] checkpoints) {
    for (int i = 0; i < pods.length; ++i) {
        pods[i].rotate(new Point(8000, 4500));
        pods[i].boost(200);
    }

    play(pods, checkpoints);
}

4.13 Comment gérer le shield ?

Ce n'est clairement pas la chose la plus compliqué à gérer. Ma classe Pod a simplement une méthode activeShield qui passe l'attribut shield à true et qui initialise un compteur de 3 tours (pour me souvenir que le pod n'a pas le droit d'accélérer pendant 3 tours).

5 L'intelligence des pods

Maintenant qu'on sait simuler les prochains tours, on peut voir plus loin. Techniquement on peut même voir aussi loin qu'on veut ! Par exemple 10 tours plus tard. Mais ce ne serait pas très utile. A partir de la, il existe plusieurs solutions. On peut tester plein de possibilités et regarder le tour suivant pour choisir la meilleur, ou même dans 5 tours. On peut être tenté de tester toutes les possibilités (mais il y en a beaucoup trop). La suite de ce document va présenter l'une des solutions possibles. Il en existe d'autres.

5.1 La fonction d'évaluation

Quelque soit la méthode qu'on va utiliser, la fonction d'évaluation est incontournable. La fonction d'évaluation prend l'étât du jeu à un instant figé et doit donner un score. C'est l'endroit le plus crucial de votre code. C'est celui qui détermine absolument tout. Il détermine le comportement de vos pods, leur façon de se déplacer, de se défendre, d'éviter les autres, de s'entraider ... Il peut déterminer aussi la façon dont vous allez prédire les déplacements adverses.

Plusieurs joueurs très haut dans le classement du contest ont expliqué ce qu'ils ont mis dans leur fonction d'évaluation. Je vais expliqué ici ce que j'ai mis dans la mienne :

Le principe est ensuite est d'ajouter des coefficients à ses différents paramètres pour arriver à quelque chose qui vous plait. Vous pouvez bien sur ajouter des paramètres, en enlever, etc ... Dans mon cas par exemple, je multiplie le premier paramètre (la différence de score des runners) par 50 pour faire en sorte que ce soit toujours le plus important.

La méthode score de ma classe Pod est assez simple. Elle ressemble à ça :

float score() {
    return checked*50000 - this.distance(this.checkpoint());
}

C'est tout simplement le nombre de checkpoint que j'ai passé multiplié par 50000 moins la distance entre le pod et son prochain checkpoint. 50000 est évidemment une valeur arbitraire. Il faut juste choisir un nombre assez grand pour que le nombre de checkpoints passés soit toujours le plus important.

Au début de chaque tour, je regarde les scores de tous les pods. Cela me permet de déterminer qui est mon runner et mon chaser. Et je fais pareil pour l'adversaire.

5.2 L'évolution génétique

L'évolution génétique est l'une des méthodes possibless pour choisir quels mouvements nos pods vont faire. Le principe est assez simple et basé sur l'évolution génétique comme on peut le trouver dans la nature. Avec la survie des plus adaptés.

Dans l'idée, on par d'une population de base de X solutions (chez moi X vaut 5, mais vous pouvez prendre une autre valeur). Chaque solution possède un score qui est sa capacité d'adaptation. Ensuite on prend certaines de ses solutions au hasard et on va les faire "muter" aléatoirement. Ou peut aussi les croiser entres elles pour en faire de nouvelles. A partir de la, il existe plusieurs implémentations possibles de l'évolution génétique :

Pour avoir essayé les 2 méthodes, c'est la première qui a donné les meilleurs résultats dans mon code.

Ensuite, il faut répéter cette opération pendant 150ms (qui est la durée maximale pour répondre par tour). Le pseudo algorithme ressemble donc à ça :

Solution[] solutions = generatePopulation();

while (time < 150) {
    Solution solution = solutions[random(0, X)].mutate();

    if (solution.score() > minScore) {
        keepSolution();
    }
}

Ce code est évidement très simplifié. Mais l'idée est la. On va rentrer un peu dans les détails maintenant

5.2.1 Qu'est qu'une solution ?

Dans mon code, une solution est une liste de couples de mouvements. Un mouvement pour le premier pod et un mouvement pour le deuxième. Pour que l'évolution fonctionne correctement, il faut qu'un movement soit complètement indépendant de l'étât de votre pod. Dans mon code, ma classe Move est faite comme cela :

class Move {
    float angle; // Entre -18.0 et +18.0
    int thrust; // Entre -1 et 200
}

J'ai ajouté quelque chose de spécial et de pas forcément très propre pour gérer les boucliers. Dans mon code j'ai défini la constante suivante : const int SHIELD = -1;. Cela m'évite de devoir gérer un attribut de plus à la classe Move et je gagne en performance. Si un Move a un thrust qui vaut -1, le pod activera son bouclier. Avoir une classe Move construite de cette façon permet d'avoir un mouvement indépendant du pod. Le pod peut se trouver dans n'importe quel état, il pourra toujours effectuer un Move quoi qu'il arrive.

Ma classe solution est donc simple elle aussi : 

class Solution {
    Move[] moves1;
    Move[] moves2;
}

moves1 sont les déplacements pour mon premier pod et moves2 sont les déplacements pour mon deuxième pod. Il vous reste à déterminer sur combien de tours vous voulez tester vos solutions. J'ai essayé plusieurs valeurs entre 5 et 10. Et c'est 6 tours qui m'ont donné les meilleurs résultats.

Il faut aussi implémenter la méthode score de Solution, qui va simuler sur le nombre de tours voulus la solution, et utiliser la fonction d'évaluation à la fin de la simulation pour connaitre le score de la solution.

float score() {
    // On joue les tours
    for (int i = 0; i < moves1.length; ++i) {
        // On applique les mouvements aux pods avant de jouer
        myPod1.apply(moves1[i]);
        myPod2.apply(moves2[i]);

        play();
    }

    // On calcul le score
    float result = evaluation();

    // On remet tout le monde au point de départ
    load();

    return result;
}

La méthode apply de mes pods ne fait qu'appliquer un mouvement au pod. Il décale l'angle et applique le thrust (ou le bouclier). Ma fonction load est ce dont j'avais parlé avant dans ce document. Après une simulation il vous faut un moyen de remettre tout le monde à l'étât initial. C'est ce que fait ma fonction load.

5.2.2 Mutations et croisements

Il existe 2 façons de faire évoluer une solution. Soit par mutation, soit par croisement.

La mutation se résume à prendre un ou plusieurs mouvements au hasard dans une solution déjà existante et à changer ce mouvement aléatoirement. Le croisement consiste à prendre 2 solutions et créer une (ou plusieurs parfois) nouvelle solution en piochant des mouvements au hasard entre les 2 solutions.

Mais attention, il ne faut pas le faire n'importe comment. Pour que l'évolution marche correctement, il faut d'abord faire de "grandes" évolutions et plus on avance, plus on fait de petites évolutions. Pour donner un exemple, voici la méthode mutate de ma classe Move :

void mutate(float amplitude) {
    float ramin = this.angle - 36.0 * amplitude;
    float ramax = this.angle + 36.0 * amplitude;

    if (ramin < -18.0) {
        ramin = -18.0;
    }

    if (ramax > 18.0) {
        ramax = 18.0;
    }

    angle = random(ramin, ramax);

    if (!this.shield && random(0, 100) < SHIELD_PROB) {
        this.shield = true;
    } else {
        int pmin = this.thrust - 200 * amplitude;
        int pmax = this.thrust + 200 * amplitude;

        if (pmin < 0) {
            pmin = 0;
        }

        if (pmax > 0) {
            pmax = 200;
        }

        this.thrust = random(pmin, pmax);

        this.shield = false;
    }
}

Comme le code le montre, j'ai un paramètre amplitude qui me sert à "doser" à quel point je veux faire muter aléatoirement un Move. Au début du tour de mon IA, ce paramètre est à 1.0 pour avoir des mutations maximales. Et plus j'avance dans mes évolutions et mes simulations, plus il devient petit avec un minimum de 0.1 à la fin du tour. Cela permet d'avoir les meilleurs résultats avec l'évolution.

Le bouclier est un cas un peu à part, j'ai juste une constante SHIELD_PROB qui indique la probabilité qu'un Move a de muter en une action d'activation du bouclier. Dans ma version finale cettte constante vaut 20.

5.2.3 Créer la population de solution de départ

Pour créer les solutions de départ, il y a plusieurs méthodes :

Dans mon code, ma population de départ est composée de 3 solutions aléatoires, 1 solution générée par une IA très simple (uniquement à base de if) et enfin je reprend la solution gagnante du tour d'avant.

Prévoir les déplacements adverses

Si vous avez bien regardé attentivement le code donné pour la fonction score de Solution, vous avez du remarquer qu'on ne fait pas bouger les pods de l'adversaire. On considère qu'ils vont juste attendre (leur angle ne change pas et ils ont un thrust de 0). Ce qui est évidemment faux puisque l'adversaire va très souvent bouger. C'est pour cela qu'il faut trouver un moyen de prévoir ses mouvements. C'est un autre point crucial de votre code. Plus vos prédictions sur les mouvements adverses seront correctes, plus votre IA sera redoutable. Dans mon cas, ma solution n'a pas été bonne. Et c'est ce qui fait que mon IA se fait complètement écraser par celle de Jeff06, de pb4608 ou encore de Owl.

Dans mon code, j'utilise mon IA très simple pour prévoir les mouvements adverses. Et ça marche mal. Mon IA est vraiment très simple et elle est souvent très loin de ce que vont faire mes adversaires. Notez que cela n'empêche pas la coopération entre vos pods (qui est rarement dépendante des mouvements adverses). Mais cela pourra empêcher votre runner d'esquiver le chaser adversaire et votre chaser n'arrivera pas à bloquer le runner adverse.

Jeff06 lui a opté pour une autre solution. Il fait une évolution génétique pour l'adversaire (en considérant que ses propres pods vont juste attendre) pendant 10ms. Il garde la meilleur solution trouvée pour l'adversaire et ensuite il fait ensuite son évolution génétique en utilisant cette solution pour prédire les mouvements adverses. Etant donné que Jeff06 a gagné le contest, je peux en déduire que sa solution est bien meilleur que la mienne !

5.3 Convertir un Move pour l'output

La dernière étape est de convertir le premier Move de la solution gagnante de l'évolution pour l'écrire dans la sortie standard. Mais la sortie standard ne peut pas prendre directement un Move composée uniquement d'un déplacement d'angle et d'un thrust. Il faut utiliser un peu de trigonométrie :

void output(Move* move) {
    float a = angle + move.angle;

    if (a >= 360.0) {
        a = a - 360.0;
    } else if (a < 0.0) {
        a += 360.0;
    }

    // On cherche un point pour correspondre à l'angle qu'on veut
    // On multiplie par 10000.0 pour éviter les arrondis
    a = a * PI / 180.0;
    float px = this.x + cos(a) * 10000.0;
    float py = this.y + sin(a) * 10000.0;

    if (move.shield) {
        print(round(px), round(py), "SHIELD");
        activateShield();
    } else {
        print(round(px), round(py), move.power);
    }
}

6 Les autres solutions

Je ne suis pas le seul à avoir utilisé un algorithme d'évolution génétique. Jeff06 , Neumann, et pb4608 l'ont fait aussi (avec plus de succès que moi car ils m'ont battu). Owl lui a utilisé la méthode du minimax / alpha beta en réduisant les possibilités à 7 coups possibles par pod. Je vous invite à aller lire leurs explications sur le forum et le blog de CodinGame